Simple Example of a Simulation in astronomix

Simple Example of a Simulation in astronomix#

Imports#

import jax.numpy as jnp

# constants
from astronomix import SPHERICAL, CARTESIAN

# astronomix option structures
from astronomix import SimulationConfig
from astronomix import SimulationParams

# simulation setup
from astronomix import get_helper_data
from astronomix import finalize_config
from astronomix import get_registered_variables
from astronomix import construct_primitive_state

# time integration, core function
from astronomix import time_integration

# plotting
import matplotlib.pyplot as plt

Simulation Setup#

Let us set up a very simple simulation, mostly with default parameters.

First we get the configuration of the simulation, which contains parameters that typically do not change between simulations, changing which requires (just-in-time)-recompilation.

config = SimulationConfig(
    geometry = CARTESIAN,
    box_size = 1.0,
    num_cells = 101,
)

Next we setup the simulation parameters, things we might vary

params = SimulationParams(
    t_end = 0.2, # the typical value for a shock test
)

With this we generate some helper data, like the cell centers etc.

helper_data = get_helper_data(config)
registered_variables = get_registered_variables(config)

Next we setup the shock initial conditions, namely

(1)#\[\begin{equation} \left(\begin{array}{l} \rho \\ u \\ p \end{array}\right)_L=\left(\begin{array}{l} 1 \\ 0 \\ 1 \end{array}\right), \quad\left(\begin{array}{l} \rho \\ u \\ p \end{array}\right)_R=\left(\begin{array}{c} 0.125 \\ 0 \\ 0.1 \end{array}\right) \end{equation}\]

with seperation at \(x=0.5\).

# setup the shock initial fluid state in terms of rho, u, p
shock_pos = 0.5
r = helper_data.geometric_centers
rho = jnp.where(r < shock_pos, 1.0, 0.125)
u = jnp.zeros_like(r)
p = jnp.where(r < shock_pos, 1.0, 0.1)

# get initial state
initial_state = construct_primitive_state(
    config = config,
    registered_variables = registered_variables,
    density = rho,
    velocity_x = u,
    gas_pressure = p,
)

config = finalize_config(config, initial_state.shape)

Automatically setting open boundaries for Cartesian geometry.

Running the simulation#

final_state = time_integration(initial_state, config, params, registered_variables)
rho_final = final_state[registered_variables.density_index]
u_final = final_state[registered_variables.velocity_index]
p_final = final_state[registered_variables.pressure_index]

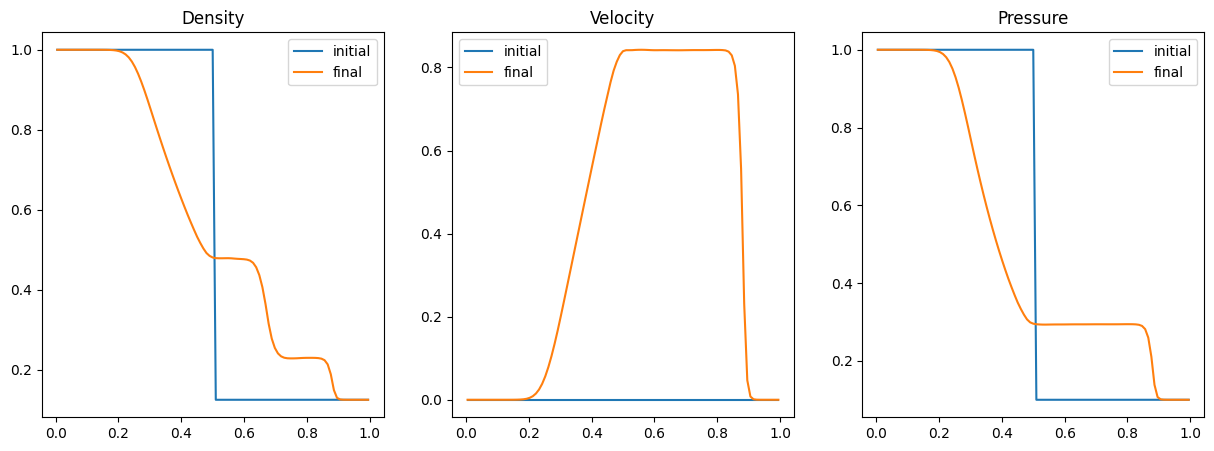
Visualization#

fig, axs = plt.subplots(1, 3, figsize=(15, 5))

axs[0].plot(r, rho, label='initial')
axs[0].plot(r, rho_final, label='final')
axs[0].set_title('Density')
axs[0].legend()

axs[1].plot(r, u, label='initial')
axs[1].plot(r, u_final, label='final')
axs[1].set_title('Velocity')
axs[1].legend()

axs[2].plot(r, p, label='initial')
axs[2].plot(r, p_final, label='final')
axs[2].set_title('Pressure')
axs[2].legend()

<matplotlib.legend.Legend at 0x74f8e86b1600>
../../_images/bd9f2855d5b1f682d66b572b1c3c2886ccd844f221c4496162aa96ae12800071.png
Contents